三维旋转激光扫描测量系统的设计(3)
2012-03-27 15:38:48   来源：   评论：0

4 转台中心轴线标定

在对三维物体进行旋转扫描测量的过程当中，通过数控转台可以实现从不同的方位对物体进行进行测量，这样才能获得被测物体全方位的外表面数据信息。然后，还需要将物体不同旋转角度的多视数据拼合在同一坐标系中。在拼合的过程当中，转台的中心轴线标定是否精确对结果有着非常重要的影响。

如图4所示，由于安装误差，转台中心轴线R与平行于z轴的z’方向难以一致，若不同角度的测量数据点绕z’旋转会产生间隙，如图5所示。

为精确标定转台中心轴线，提出如下方案：在图4的转台上固定一个标定球。通过数控系统控制转台旋转，控制球的球心绕转轴R形成一个圆，该圆的圆心O"是R上的点，该圆所在平面的法矢即为R的方向。

基于该思路，在xyz三轴测量系统中测量并计算标定球三个不同位置的球心P1(x1，y1，z1)，P2(x2，y2，z2)，P3(x3，y3，z3)，P1，P2，P3所在平面的法矢量N即为转台中心轴线的方向。

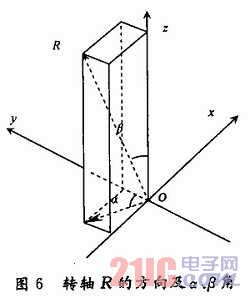
有了转台中心轴线的方向，还需要确定空间三点P1，P2，P3绕转轴R形成圆的圆心O"(x0，y0，z0)才能使转台中心轴线定位。如图6，为了求O"，首先计算转轴R在xOy面上的投影与y轴夹角α、R与z轴的夹角β，然后P1，P2，P3依次绕z轴、x轴旋转到与xOy平行的平面上，旋转矩阵分别为：

式中：P1，P2，P3旋转到与xOy平行的平面上就可以很容易求出圆心，然后将圆心再依次绕x轴、z轴反向旋转β和α，即得到O"，转台中心轴线的方向和位置得到确定。

5 多视拼合及重叠数据区域的处理

逆向工程中，对实物样件进行数字化时，因为测量范围的限制或遮挡的关系，往往不能在同一坐标系下一次测量产品全部的几何数据，需要在不同的方位(即不同的坐标系)测量产品的各个部分，其中每个方位测量的数据片称为视，多个方位测量的数据称为多视数据，将不同坐标系下的多视数据统一到同一坐标系下的处理过程，称为多视数据拼合。

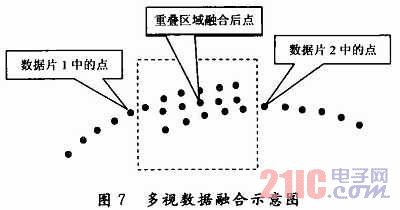
多视数据拼合包括两个部分，第一步是将不同坐标系的数据变换到同一个坐标系中，数据片通过旋转和平移来调整方位达到形位匹配；多视数据变换到同一坐标系后，数据片之间存在重叠区域，由于测量和变换存在误差，重叠区域内的多重数据需要做合理的运算使其融合为单层数据。第一步是方位调整，可称为“拼”(Registration)，亦称数据对齐，第二步是多层数据融合为单层数据，可称为“合”(Intergr-ati-on)。将数据点集看作一个刚体，两个数据点集的对齐属于空间刚体移动，因此多视数据对齐问题可看作空间两个刚体的坐标转换，问题归结为求解相应的转换矩阵，移动矩阵T和旋转矩阵R。如图7所示是2个数据片截面上两行数据融合的示意图。最简单的融合方法是中值平均，这样会在重叠区域边缘出现台阶。改进的方法是加权，使得融合后的数据片在重叠区域边缘光滑过渡，但这种方法未考虑重叠区域边缘外一定邻域内的数据点也存在误差。

6 结语

通过激光旋转扫描测量的方式获取样件的三维信息，可方便快捷地进行雕刻制品的加工，快速实现雕刻艺术品的数字化以及复制或批量生产。从而节省硬件平台及人力成本，在木雕、石雕、玉雕等各类雕刻行业中获得极其广泛的应用，掀起了一场革新的浪潮。